実験1/物理学実験
想い出の名古屋工業大学
想い出の名古屋工業大学
こひつじの家
名古屋工業大学(名工大)に勤務していたときに授業を担当した「物理学実験」でおこなわれていた,実験1「ノギスとマイクロメータ」の参考資料です。
【注】実験内容等が変わっている可能性がありますので,あくまでも参考程度に見てください。
【注】実験内容等が変わっている可能性がありますので,あくまでも参考程度に見てください。
最終更新:2007-10-11
| 注意 試料のさび 試料の表面にさびがあったら申し出てください。あたらしい試料と交換します。 注意 ノギスで主尺目盛を読み取る位置 主尺目盛は副尺目盛の「0」の位置で読み取る。まちがえてスライダの左端で読み取らないように。図 1-1 における主尺目盛の読みは 17 mm ではないよ! |
 図 1-1 ノギスの読み |
|
読み取った値は 18.65 mm となる。 注意 マイクロメータの操作法 私がいくつかのマイクロメータを慎重に操作してテストしたところ,ゼロ点の読みはほとんどバラつかず,読みの変動幅は±0.001 mm に収まることがわかった(表 1-1)。 |
表 1-1 マイクロメータのゼロ点
|
| ゼロ点の読みがバラついた場合は,スピード違反の可能性が大きい。 |
 図 1-2 測定対象物をはさんだマイクロメータ |
|
シンブル(ラチェット)を右に回していくとスピンドルも回転しながら前進し,やがてスピンドルが測定対象物かアンビルに接触する。接触した瞬間もシンブルなどは回転を続けようとするので,接触した部分にはシンブルなどがもっていた回転運動量に比例した力が生じ,測定対象物やフレームなどが変型する。この変型がマイクロメータの最小目盛 0.001 mm 以下であれば問題にならないが,回転運動量が大きい場合には変型が 0.001 mm よりも大きくなり,測定誤差が生じる。 スピンドルを測定対象物やアンビルに接触させるときは,シンブル(ラチェット)を目に見えないほどゆっくりと回さなければならない。スピード違反は事故のもとである。 参考 2種類のマイクロメータがある 購入時期のちがいによって2種類のマイクロメータがある。新しいタイプはシンブルにもラチェット機構が設けてあるので,測定時にシンブルをつまんで回すことができる。さらにラチェット機構に摩擦式(フリクション式)が用いられているため,空回りしたときにガリガリという音がしない。 参考 ノギスとカリパー 名工大の物理学実験では2002年度までノギスのことをカリパーとよんでいた。カリパーという名称は1969年に発行した「物理実験指導書」初版から使用され続けてきたが,調べてたところ現在その名称は使われておらず,一般にノギスとよばれていることがわかった。日本工業規格(JIS)でもノギスという名称が使われている。 ただし英語では slide calipers(スライド式内外径計測器)や vernier calipers(副尺付内外径計測器)であるので,日本でもキャリパーとよばれることがある。ちなみにノギスだが,これはドイツ語の Nonius(副尺)からきている。 ヒント-1 Δh/h 等の有効数字 Δh/h や 2Δd/d は相対誤差だから,たとえば Δh/h = 0.001 または Δh/h = 0.0010 というように,有効数字は 1〜2 桁が適切である。 ヒント-2 図示の効果 「ふたつの測定結果が誤差を考慮して一致しているかどうか」については,文章や式を使って表すよりも,図1-3のようにそれぞれの「最確値±誤差」を図示した方が,はるかにわかりやすい。 |
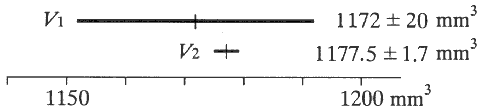 図1-3 誤差を考慮した体積 |
| ヒント-3 誤差が与える影響とは まず最初に,見積もられた誤差は非常におおまかな量であることを認識する必要がある。つぎに誤差という量の比較であるが,たとえば Δh/h = 0.001(A),2Δd1/d1 = 0.02(B),2Δd2/d2 = 0.0007(C)となった場合,BはAの20倍もあるから顕著な違いがあるといえる。しかしBはCの1.5倍ほどしかないので顕著な違いがあるとはいえない。たとえで示すと,A氏は約束などの時間に3分ほどルーズ,B氏は1時間ほどルーズ,C氏は2分ほどルーズで,ルーズさは誤差に相当する。実際問題としてA氏とC氏のルーズさの違いは人に知られないほどであろうが,B氏のルーズさは人々に大きな影響を与えてしまう。 ヒント-4 分布図の描き方1 分布図は,図1-4の右側のように棒グラフと棒グラフの間を空けずに描く。 |
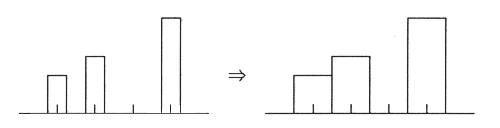 図1-4 棒グラフの間隔 |
| ヒント-5 分布図の描き方2 この実験で作成する分布図においては,図1-5のように物理量(ここでは直径)の目盛と数値は,棒グラフの中央に置く。 |
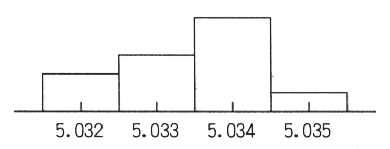 円柱の直径 d2 [mm] 図1-5 マイクロメータで測定した測定値の分布 |
| 考えてみよう その 1
測定 1 は円柱の直径を機器誤差が 0.05 mm のノギスで,測定 2 は機器誤差が 0.002 mm のマイクロメータで測定したので,直径の誤差については測定 1 に比べて測定 2 の方が 1 桁以上も小さくなることは理解しやすい。しかし高さについては共に機器誤差が大きい方のノギスで測定したにもかかわらず,求められた体積の誤差も測定 1 に比べて測定 2 の方が 1 桁も小さくなっている。すなわち高さの測定誤差は,直径の測定誤差に比べて体積に与える影響が小さい。これはどのように考えたらよいだろうか。 ⇒ヒント 考えてみよう その 2 直径も高さもマイクロメータで測定したとして,これを測定 3 としよう。測定 3 によって得られた円柱の体積の誤差は,測定 2 によって得られた体積の誤差に比べてどれだけ小さくなるだろうか。その結果から,測定 3 の価値を評価してみよう。 ⇒ヒント 考えてみよう その 3 測定試料が,高さ 2 mm,直径 25 mm という硬貨のような円盤だったとしたら,どちらをノギスで,どれをマイクロメータで測定するとよいだろうか。 ⇒ヒント 実験 1 について 測定試料として与えられた円柱は「ピンゲージ」と呼ばれる標準ゲージで,側面に表示されている寸法(単位はmm)に対して ±0.001 mm という精度で精密に作られている。ということで,ノギスやマイクロメータが正常で,それらを正しく用いた場合には,「測定値±機器誤差」にゲージの寸法が入っている可能性が大きい。というわけで実験 1 は,みなさんの測定技術を試すという意地の悪い実験でもあ〜る。 この実験の問題点としては試料が精密すぎることがあげられる。よほど乱暴な測定をおこなわないかぎり,偶然誤差が機器誤差に比べて無視できるほどに小さくなってしまうので,誤差を見積もるためのテーマ実験としてはやや不適切だ。 この実験をとおして,マイクロメータの目盛は読み取りにくく,読み取り間違いをしやすいことが分かったと思う。これからマイクロメータで測定するときには,ものさしやノギスでも測ってみることを心がけてほしい。せっかく 0.001 mm の位まで精密に測定しても,1 mm や 0.1 mm の位を読みまちがえては,お笑いにもならない。 記:2005-11-12 |