
最終更新:2009-11-17
新規作成:2007-12-09
新規作成:2007-12-09
3 周辺を縮小
広角歪みを補正する
広角歪みを補正する
デジカメ実験室
トップページ > 科学と技術の部屋 > デジカメ実験室 > 周辺を縮小
[2 画角]のページを見ると,広角レンズ,特に超広角レンズで撮影した写真は,大きく拡大してよほど近くから見ないかぎり歪んで見えてしまうことがわかる。しかし実際にそのような条件で写真を見ることはなかなか困難である。できることなら,ごく普通の大きさの写真で,歪んでいないように見えたらよいと思う。もちろん広角レンズで撮影した広い視野は保たれていなければいけない。
それでは広角レンズで撮影したの歪みを感じさせないようにする方法があるのかどうか,あるとしたらどうしたらよいか考えてみよう。
広角レンズで撮影した写真では,写真の中心部に比べて周辺部が大きく写っていることについては[レンズの歪み?]のページで簡単に説明したが,ここでもう少し詳しく調べることにする。
図3-1は,光軸から角度θの方向にある視角δの被写体を,焦点距離fのレンズによって撮影素子上に結像させたものである。このとき光軸上の位置から像のできる位置までの距離をa,大きさ(長さ)をdとする。
それでは広角レンズで撮影したの歪みを感じさせないようにする方法があるのかどうか,あるとしたらどうしたらよいか考えてみよう。
広角レンズで撮影した写真では,写真の中心部に比べて周辺部が大きく写っていることについては[レンズの歪み?]のページで簡単に説明したが,ここでもう少し詳しく調べることにする。
図3-1は,光軸から角度θの方向にある視角δの被写体を,焦点距離fのレンズによって撮影素子上に結像させたものである。このとき光軸上の位置から像のできる位置までの距離をa,大きさ(長さ)をdとする。
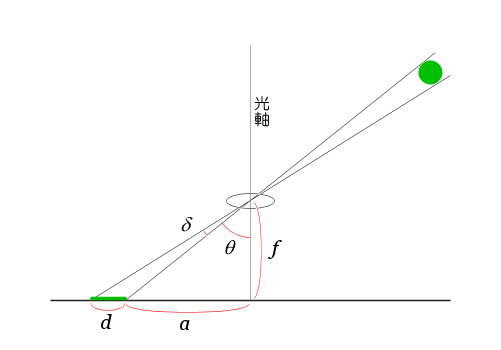 図3-1 光軸からの距離と像の大きさ
図3-1 光軸からの距離と像の大きさ
このとき像のできる距離aは,
となり,像の大きさdは,
で表すことができる。そしてδが十分に小さいときは微分形
で計算することができる。
例として,焦点距離f=15mm(35mm判換算)のレンズで,視直径0.5度の満月を撮影した場合について式(3-3) を使って計算してみると,光軸上(θ=0)での像は直径0.13mmの円となるが,撮影素子の長辺の最も外側では式(2-1) からθは50度となるので,長径が0.32mmで短径が0.20mmの楕円
*1
(厳密には楕円ではない) になってしまう。本来は丸いはずの満月が楕円となって写っているので,写真を見た場合に不自然に感じる(レンズの焦点距離は35mm判換算値で示している)。
式(3-3)によると,光軸からの角度θが大きくなるにしたがって1/cos2θという関係で像が引き伸ばされていくことがわかるが,角度θよりも撮影素子の中心からの距離aを用いた方がわかりやすいので,式(3-1) と式(3-2) を使ってまとめると,
*2
という関係が求められる。ここでmは撮影素子の中心と像の位置とを結んだ直線方向における拡大率である。
ここでも撮影素子の大きさが35mm判相当(36mm×24mm)で,レンズの焦点距離fが15mmの場合について,式(3-4) を用いて拡大率を計算してみると,撮影素子の左右端(a=18mm)では2.44,対角端(a=21.6mm)では3.07となる。撮影素子の中心から左右端までの距離を100とした場合の,位置と拡大率の関係を計算して,表3-1に示した。表3-2はレンズの焦点距離と拡大率との関係である。
| a=ftanθ | (3-1) |
| d=f[tan(θ+δ)−tanθ] | (3-2) |
| d=f[1/cos2θ]δ | (3-3) |
例として,焦点距離f=15mm(35mm判換算)のレンズで,視直径0.5度の満月を撮影した場合について式
短径についてはf[1/cosθ]δで計算した。光軸上の像の直径もこの式で計算できる。
式(3-3)によると,光軸からの角度θが大きくなるにしたがって1/cos2θという関係で像が引き伸ばされていくことがわかるが,角度θよりも撮影素子の中心からの距離aを用いた方がわかりやすいので,式
tan-1の微分形になる。
| m=1+(a/f)2 | (3-4) |
ここでも撮影素子の大きさが35mm判相当(36mm×24mm)で,レンズの焦点距離fが15mmの場合について,式
| 位置 | 拡大率 | 備考 |
| 0% | 1 | 中心 |
| 25 | 1.09 | |
| 50 | 1.36 | |
| 75 | 1.81 | |
| 100 | 2.44 | 左右端 |
| 120 | 3.07 | 対角端 |
| 焦点距離 | 左右端 | 対角端 |
| 15mm | 2.44 | 3.07 |
| 20 | 1.81 | 2.17 |
| 28 | 1.41 | 1.60 |
| 35 | 1.26 | 1.38 |
| 50 | 1.13 | 1.19 |
| 75 | 1.06 | 1.08 |
| 100 | 1.03 | 1.05 |
| 200 | 1.01 | 1.01 |
表3-1を見ると,短焦点の広角レンズでも中心に近いところではほとんど歪んだように見えなくて,中心から離れたところでは大きく歪んでいるように見えることがわかる。また表3-2を見ると,焦点距離の長いレンズでは周辺部分でも歪んだようには見えないことがわかる。
さて本題の「広角レンズで撮影したの歪みを感じさせないようにする方法」を模索することだが,手持ちの画像処理ソフトPaint Shopを使って実験してみた。
Paint Shopには画像を変形させるいくつかの機能があるが,いろいろためしてみたところ目的に合った機能としては[効果]→[歪み効果]→[膨張]が使えそうであることがわかった。[膨張]は写真の中心を膨張させる機能で,相対的に周辺部が縮小されることになる。実験には今までにもたびたび登場した15mmの超広角レンズで撮影した部屋の写真を用いることにする。写真のサイズはひとまわり小さくした。図3-2は処理をする前で,図3-3,図3-4,図3-5は[膨張]機能の[強さ]をそれぞれ30,50,70で処理した写真である。
さて本題の「広角レンズで撮影したの歪みを感じさせないようにする方法」を模索することだが,手持ちの画像処理ソフトPaint Shopを使って実験してみた。
Paint Shopには画像を変形させるいくつかの機能があるが,いろいろためしてみたところ目的に合った機能としては[効果]→[歪み効果]→[膨張]が使えそうであることがわかった。[膨張]は写真の中心を膨張させる機能で,相対的に周辺部が縮小されることになる。実験には今までにもたびたび登場した15mmの超広角レンズで撮影した部屋の写真を用いることにする。写真のサイズはひとまわり小さくした。図3-2は処理をする前で,図3-3,図3-4,図3-5は[膨張]機能の[強さ]をそれぞれ30,50,70で処理した写真である。
 図3-2 15mm超広角レンズで撮影した部屋
図3-2 15mm超広角レンズで撮影した部屋 図3-3 膨張強度30で処理した写真
図3-3 膨張強度30で処理した写真 図3-4 膨張強度50で処理した写真
図3-4 膨張強度50で処理した写真 図3-5 膨張強度70で処理した写真
図3-5 膨張強度70で処理した写真
実際の部屋と見比べたりした感じでは,強さ50あたりが最もよさそうに思える。しかしキーボードや地球儀などが相変わらず歪んだように見えるし,まだ不自然である。そこで[膨張]機能がどのような割合で画像を変形させているかを,[1 レンズの歪?]のページで使用したテストチャートを強さ50で膨張させて調べてみた。
 図3-6 強さ50で膨張させたテストチャート
図3-6 強さ50で膨張させたテストチャート
[膨張]機能を使うことによって確かに中央部が膨らんで見えるようになったが,膨張させるための関数が広角レンズによる周辺拡大を打ち消す形になっていないことがわかった。表3-1を見ると広角レンズで撮影したときは写真の中央部の変形はほとんどなく,中央から遠くなると急激に拡大されているのに対して,画像処理で[膨張]させたパターンは中央からの距離に比例するように小さくなっている。したがって[膨張]機能によっては十分に補正することができないことになる。
Paint Shopの[歪み効果]には[膨張]以外に[レンズの歪み]というものがあり,その中の[魚眼]と[樽型]が相対的に画像の周辺部を小さくする機能である。[魚眼]には[視野]というパラメータがあり,視野を大きくするほど強く変形させることができるが,超広角レンズで撮影した写真を視野90度で変形させたところ,図3-7が得られた。テストチャートを同様な処理で変形させると図3-8のようになる。
Paint Shopの[歪み効果]には[膨張]以外に[レンズの歪み]というものがあり,その中の[魚眼]と[樽型]が相対的に画像の周辺部を小さくする機能である。[魚眼]には[視野]というパラメータがあり,視野を大きくするほど強く変形させることができるが,超広角レンズで撮影した写真を視野90度で変形させたところ,図3-7が得られた。テストチャートを同様な処理で変形させると図3-8のようになる。
 図3-7 視野90度で魚眼変形させた写真
図3-7 視野90度で魚眼変形させた写真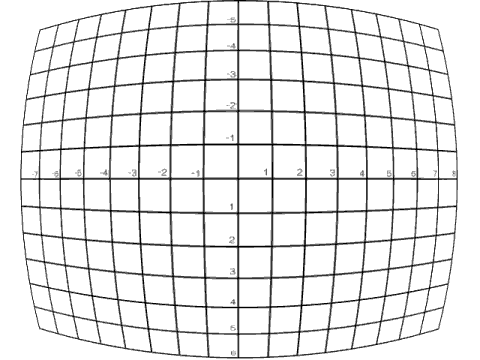 図3-8 視野90度で魚眼変形させたテストチャート
図3-8 視野90度で魚眼変形させたテストチャート
四角い物体が丸みを帯びているし,特に周辺部が湾曲して樽型(たるがた)になっているが,地球儀はちゃんと丸くなっていて,ディスプレイの縦横比やキーボードも自然な形になっている。湾曲さえなければよいのだが。
湾曲を取り除くために[樽型歪みの補正]という機能を使ってみたところ,超広角レンズで撮影した元の写真に近い状態に戻ってしまった。いろいろためしてみたところ[魚眼]と[膨張]で加工してから[樽型歪みの補正]で丸みを取り去ると,なんとか見られるような写真ができあがることがわかった。視野90度の[魚眼]で変形させてから,強さ40の[膨張]で変形させ,強さ100の[樽型歪みの補正]をかけて,さらに強さ60の[樽型歪みの補正]をかけた写真が図3-9,同様な処理でテストチャートを補正したものもが図3-10である。
湾曲を取り除くために[樽型歪みの補正]という機能を使ってみたところ,超広角レンズで撮影した元の写真に近い状態に戻ってしまった。いろいろためしてみたところ[魚眼]と[膨張]で加工してから[樽型歪みの補正]で丸みを取り去ると,なんとか見られるような写真ができあがることがわかった。視野90度の[魚眼]で変形させてから,強さ40の[膨張]で変形させ,強さ100の[樽型歪みの補正]をかけて,さらに強さ60の[樽型歪みの補正]をかけた写真が図3-9,同様な処理でテストチャートを補正したものもが図3-10である。
 図3-9 魚眼→膨張→樽型歪補正で補正した写真
図3-9 魚眼→膨張→樽型歪補正で補正した写真 図3-10 魚眼→膨張→樽型歪補正で補正したテストチャート
図3-10 魚眼→膨張→樽型歪補正で補正したテストチャート
このようにして補正すると,キーボードも左下の方にあるコーヒーカップも,単純に[膨張]だけの処理をしたときよりも自然な形に見えるようになっている。しかしこの方法はいつでも使うことができるのだろうか?たとえば撮影素子に平行な平面被写体を写した場合には補正が不必要なのだから,補正することによって歪んでしまうことになる。それは極端としても,カメラの前に横一列に並んだ人物写真を撮ったときの補正もこの方法で良いのだろうか?
ということで[レンズの歪み?]のページにもあった一列に並んだマーカーについても同様の補正をおこない,補正前後の写真を比較してみた。
ということで[レンズの歪み?]のページにもあった一列に並んだマーカーについても同様の補正をおこない,補正前後の写真を比較してみた。

図3-11 補正する前のマーカーの写真
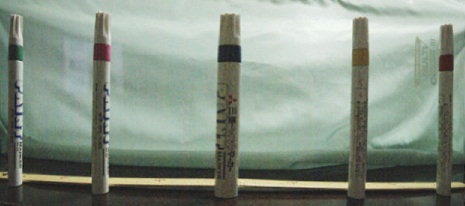 図3-12 魚眼→膨張→樽型歪補正で補正したマーカーの写真
図3-12 魚眼→膨張→樽型歪補正で補正したマーカーの写真
だめではないか! こんどは逆に中央に近いほど太くなってしまった。
おかしくなってしまった理由は簡単である。式(3-4)までは,視角δが一定であるとして考えてきたが,カメラの前に横一列に並んだ被写体の場合は並んだ位置によって被写体までの距離が異なるため,視角が変わってしまうからだ。
レンズからの距離がeで,撮影素子に平行な直線上に置かれた,半径rの球を撮影した場合を図3-13に示す。その他の条件は図3-1のときと同じである。
おかしくなってしまった理由は簡単である。式(3-4)までは,視角δが一定であるとして考えてきたが,カメラの前に横一列に並んだ被写体の場合は並んだ位置によって被写体までの距離が異なるため,視角が変わってしまうからだ。
レンズからの距離がeで,撮影素子に平行な直線上に置かれた,半径rの球を撮影した場合を図3-13に示す。その他の条件は図3-1のときと同じである。
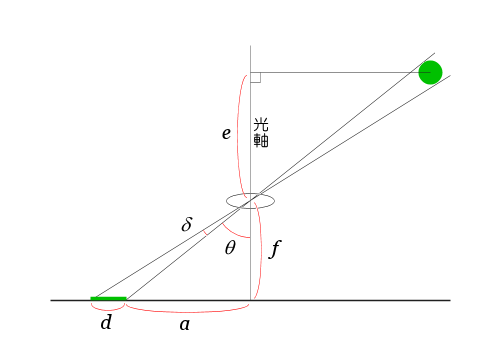 図3-13 被写体が直線上に並んでいるときの像の大きさ
図3-13 被写体が直線上に並んでいるときの像の大きさ
被写体の大きさが被写体までの距離に比べて十分に小さいとすれば視角δは,
で表すことができるので,式(3-3)と式(3-1)を用いて,
が求められる。焦点距離f=15mmの超広角レンズを用いて撮影したときの,位置と拡大率の関係を式(3-6)を使って計算し,表3-3に示した。位置については撮影素子の中心から左右端までの距離を100とした。表3-4はレンズの焦点距離と拡大率との関係である。
| δ=2rcosθ/e | (3-5) |
| δ=2rf/(ecos(tan-1(a/f))) | (3-6) |
| 位置 | 拡大率 | 備考 |
| 0% | 1 | 中心 |
| 25 | 1.04 | |
| 50 | 1.17 | |
| 75 | 1.35 | |
| 100 | 1.56 | 左右端 |
| 120 | 1.75 | 対角端 |
| 焦点距離 | 左右端 | 対角端 |
| 15mm | 1.56 | 1.75 |
| 20 | 1.35 | 1.47 |
| 28 | 1.19 | 1.26 |
| 35 | 1.12 | 1.18 |
| 50 | 1.06 | 1.09 |
| 75 | 1.03 | 1.04 |
| 100 | 1.02 | 1.02 |
| 200 | 1.00 | 1.01 |
表3-1と表3-3,または表3-2と表3-4を見比べると,一直線上に置かれた被写体の場合は拡大率が小さいことがわかる。そこでマーカーが並んでいる図3-11の写真について,中央と両端のマーカーがほぼ同じ太さになるように,[膨張]機能の強さを調節して処理をしてみた(図3-14)。このときの[膨張]の強さは25だった。
 図3-14 強さ25で膨張させたマーカーの写真
図3-14 強さ25で膨張させたマーカーの写真
このように比較的簡単な補正によって,かなり自然な感じにすることができた。ただし,よく見ると等間隔には並んでないし,2本目と4本目のマーカーが少し細いような気もする。
超広角レンズで撮影した人物写真でテストしてみよう。図3-15は結婚披露宴で撮影した集合写真である。これ以上うしろに下がることができなかったので15mmの超広角レンズを使用した。 *3
超広角レンズで撮影した人物写真でテストしてみよう。図3-15は結婚披露宴で撮影した集合写真である。これ以上うしろに下がることができなかったので15mmの超広角レンズを使用した。 *3
本撮影の前に写した写真である。
 図3-15 超広角レンズで撮影した集合写真
図3-15 超広角レンズで撮影した集合写真
図3-15を見ると,やはり中央付近の人に比べて端にいる人が太ったように写っている。この写真に対して,マーカーのときと同様に強さ=25の[膨張]で処理をしたものが図3-16である。
 図3-16 膨張機能で処理した集合写真
図3-16 膨張機能で処理した集合写真
同じ列に並んでいる人たちを見比べると,顔の大きさや形がほぼ自然な状態になっている。後列の人が極端に小さくなってしまうという広角レンズの欠点を補うことはできないが,補正の効果は大きい。
図3-17は超広角レンズを使用して真横から撮影した気動車である。このように平面的な被写体を正面から撮影した写真に対しては,補正の必要はなさそうだ。
図3-17は超広角レンズを使用して真横から撮影した気動車である。このように平面的な被写体を正面から撮影した写真に対しては,補正の必要はなさそうだ。
 図3-17 超広角レンズで写した気動車
図3-17 超広角レンズで写した気動車
これまでの実験などによって,広角レンズで撮影した写真が歪んで見えないように補正する方法は,被写体によって違うことがわかってきた。一般的な写真はタイプの異なる被写体が混在しているので,全ての被写体が歪んで見えないように補正することは不可能に近いであろう。最も大切な被写体が歪んで見えないように,いろいろ試してみる必要がありそうである。
| *1 | 短径についてはf[1/cosθ]δで計算した。光軸上の像の直径もこの式で計算できる。 |
| *2 | tan-1の微分形になる。 |
| *3 |
本撮影の前に写した写真である。
|